［論文紹介］Neuro-Symbolic Execution: Augmenting Symbolic Execution with Neural Constraints (NDSS 2019)

はい、シンボリック実行だいすきクラブの友利奈緒です。通勤中に論文を読んでる系の女の子なのですが、ここ半年は本を読んでいたので論文サーベイがすっかりご無沙汰になっていました＞＜

Semantic Scholarから送られるSymbolic Executionタグのアラートを半年眺めていた限りでは、Blockchainのスマートコントラクトの検証（Verification）やJavaScript・Javaのシンボリック実行が多かった印象でしたが、調べてみると面白い論文が出てました。シンボリック実行はまだまだ盛り上がっててよかったです…>_<…

Neuro-Symbolic Execution: Augmenting Symbolic Execution with Neural Constraints (NDSS 2019)
- シンボリック実行において脆弱性の発現条件の導出と充足が困難な問題をニューラルネットワークで解決した。
- ニューラルネットワークを用いて制約充足問題を解く。（文面からして謎テクノロジーｗ）
- 2018年7月に内容がよく似た論文が同じ著者から出ている [1807.00575] Neuro-Symbolic Execution: The Feasibility of an Inductive Approach to Symbolic Execution
Symbolic Execution for Deep Neural Networks (2018)
- 多層パーセプトロンのクラス分類で決定要因になっている1、2ピクセルの検出。
- どこかの学会を通った論文ではない？
- 実験で使用したコードは公開されてないっぽい
Concolic Testing for Deep Neural Networks
- https://github.com/TrustAI/DeepConcolic

今回は今年のNDSS（コンピュータセキュリティの学会系トップカンファレンス）で採択された "Neuro-Symbolic Execution: Augmenting Symbolic Execution with Neural Constraints" の論文紹介です。リンク先には論文とスライドと発表動画があります。

https://www.ndss-symposium.org/ndss-paper/neuro-symbolic-execution-augmenting-symbolic-execution-with-neural-constraints/

論文では言及されていないが、私が補足が必要と思って書き足したところには「友利注」を付けます。

シンボリック実行の説明は省略します。シンボリック実行には数種類のアルゴリズムがあるのですが、一般に言われるシンボリック実行の説明は以下のスライドの9～15ページ目を読むとだいたい分かると思います。

speakerdeck.com

背景
やったこと
コンセプト
アプローチ詳細
評価
結論
所感
付録：多層パーセプトロンの復習

背景

本論文で着目している、シンボリック実行における問題は次の3つ。

制約導出の困難さ
- 一般に目的の状態（本論文では特定箇所の脆弱性）が発現する地点に到達するのが難しい
  - 例）複雑なループ
    - 友利注：ループがn個あり1個のループが高々m回で抜けられるならば、状態数は $O(m^n)$ 。基本無理ゲー
  - 要はパス爆発（Path Explosion）問題に直面する
制約ソルバーの限界
- KLEEは浮動小数点に非対応。最近のSTPとZ3は浮動小数点に対応しているがとても遅い。
  - 友利注：整数よりも実数が圧倒的に探索空間が広いので遅いのは仕方ないかも。
- 浮動小数点をBitVector（SMTにおけるバイナリ値の表現形式）として扱っても実用的な時間内で充足できなかった。
実行対象のコードの欠損
- シンボリック実行エンジン（が採用しているライブラリ）が実行対象で呼び出される一部の関数に対応していない（シンボリック実行あるある）。
  - 友利注：シンボリック実行エンジンはライブラリ関数の呼び出しに対し、通常実行で使用されるライブラリ（glibcなど）の代わりに簡易なライブラリを用意して対処する。
    - KLEEはuClibcという簡易で軽量なlibcを採用しているが、全部のlibc関数には対応していない（本論文の場合はfabs）。
    - angrはsymbolic summaryと呼ばれるlibcの各関数の作用をシンボリックに表現した関数を取り揃えているが、全部のlibc関数には対応していない。

やったこと

Newro-symbolic実行エンジンNeuExを実装した。NeuExは脆弱性の候補箇所（CVP; Candidate Vulnerability Point) に対して、脆弱性を発現する入力（Crash Inputs; Validated Exploits）を生成する。

コンセプト

本論文では先の困難に対して以下のアプローチを取った。

(1) シンボリックモードとニューロンモードの2つの実行モードを持つ
- シンボリックモードは従来シンボリック実行
- シンボリックモードが行き詰まるとニューロンモードに移行
  - 4種類の移行条件：(a) モデル化されていないAPIの呼び出し (b) ループの繰り返し数が上限値に到達 (c) Z3がタイムアウト (d) メモリ使用量が上限値に到達
- ニューロンモードでは入力は具体値。制約をニューラルネットワークで内包し、制約を満たす入力（実行対象への入力）と出力（制約式で拘束された変数）の組を学習する。
  - 友利注：クラス分類問題ではない。あくまで関数 $N: x \mapsto y$ の表現方法を学習するだけ（回帰問題）。
(2) シンボリック制約を多層パーセプトロンにより近似解で求める
- シンボリック制約は誤差関数に変換される
- 解の導出方法はニューロンモードで述べたとおり。

Neuro-symbilicのアイデア（ニューラルネットワークとシンボリック実行の組み合わせ）は新規。先行研究（友利注：引用されている範囲では不変式（Invariant）に関するもの）では制約の導出にシンボリック実行ではない帰納的なアプローチが取られていたが、1つもニューラルネットワークを採用していなかった。

アプローチ詳細

システム構成

f:id:katc:20190608193341p:plain — Fig. 4

Neural Modeの構成

f:id:katc:20190608193225p:plain — Fig. 5

以下の要領でニューラルネットワークの訓練データ $(\mathbf{x}, \mathbf{y}$ ) （論文の表記は $(\mathbf{I}_i, \mathbf{O}_i)$ ）を得る。

Neural Modeに移行後、NeuExはコールグラフを参照し、現在のシンボリック状態でパス上では到達可能なCVPを選出する。
着目している分岐（友利注：原文ではsymbolic branch。【何のこと？】）を始点、着目するCVPを終点として、始点から終点までを実行する。
- 入力はシンボリック制約から生成された具体値をシードとしてランダム生成されたもの（たいてい10万個）
- 入力のうちいくつかは終点に到達する（友利注：このとき $\mathbf{x}$ と $\mathbf{y}$ の対応を得られる）
- 友利注：終点はCVPにおける制約式で拘束された変数 $\mathbf{y}$ を含むことに注意

Neural-symbolic制約の充足

NeuExはNeural-symbolic制約充足にSymSolvとNeuSolvと呼ばれる2種類の制約ソルバーを組み合わせる。

SymSolv

SymSolvはいわゆるSMTソルバーが対応するような制約式を取り扱う制約ソルバー。

NeuSolv

論文とスライドの書き方がわかりにくいので、NeuSolvについては全面友利注とする。【注意：本論文・スライド・発表動画を参照した上でエスパーした内容が多分に含まれる上に、私の数学力不足に起因する誤りがある可能性がある】

NeuSolvは、ニューラル制約を数値解析における最急降下法により解く。

ニューラルネットワークは先の学習により関数 $N: \mathbf{x} \mapsto \mathbf{y}$ を自身のネットワークにより表現可能となっている。ここで、あるCVPのシンボリック制約を式 $C(\mathbf{y}) = 0$ とする。NeuExはこれをロス関数 $L(\mathbf{y})$ （友利注：ニューラルネットワークの学習におけるロス関数とは別物）に変換する。

ロス関数 $L$ は以下の性質を持っている。

制約を充足するまでは $\nabla L$ が非ゼロ
下限が存在
- でないと探索が停止しない
友利注：関数 $N, L$ について、 $N: \mathbf{R}^n \rightarrow \mathbf{R}^m, \quad L: \mathbf{R}^m \rightarrow \mathbf{R}$

ロス関数の性質から、以下を満たす $\mathbf{\hat{x}}$ はCVPの制約を満たす。

$L(N(\mathbf{\hat{x}})) = \min(L(N(\mathbf{x}))$

上の非線形方程式を解くために数値解析で用いられる以下の最急降下法を用いる（ $k$ は反復回数）。

${\mathbf{x}}^{(k+1)} = {\mathbf{x}}^{(k)} + \epsilon \nabla L (N(\mathbf{x}^{(k)}))$ （これは論文の式(5)）

問題は $\nabla L (N(\mathbf{x}))$ が計算可能かどうかである。

$\mathbf{y} = N(\mathbf{x}), z = L(\mathbf{y})$ とすると、

$\nabla L (N(\mathbf{x})) = \left[\dfrac {\partial z}{\partial x_0}, \cdots, \dfrac {\partial z}{\partial x_i}, \cdots, \dfrac {\partial z}{\partial x_n}\right]^T .$

ここで連鎖律により、

$\dfrac {\partial z}{\partial \mathbf{x}} = \dfrac {\partial z}{\partial (y_1, \cdots, y_ m)} \dfrac {\partial (y_1, \cdots, y_j, \cdots, y_ m)}{\partial (x_1, \cdots, x_i, \cdots, x_n)} = \nabla L(\mathbf{y}) \dfrac{\partial N}{\partial \mathbf{x}}$ (*1)

であることに注意すると、 $\nabla L(\mathbf{y}) = \left [ \dfrac{\partial L(\mathbf{y})}{\partial y_1}, \cdots, \dfrac{\partial L(\mathbf{y})}{\partial y_m} \right]^T$ は $L$ の定義（Table II）から導出可能であり、また

$\dfrac{\partial y_j}{\partial x_i} = \dfrac {\partial N_j(\mathbf{x}) }{\partial x_i} \approx \dfrac{ N_j(x_1, \cdots, x_i + \Delta x_i, \cdots, x_n) - N_j(x_1, \cdots, x_i, \cdots, x_n)}{\Delta x_i}$

であるから、 $\nabla L (N(\mathbf{x}))$ は計算可能。

(*1) $\dfrac{\partial N}{\partial \mathbf{x}}$ はヤコビ行列

（本当にこれで合ってるのだろうか？ $\nabla L (N(\mathbf{x}))$ の計算方法の説明がどこにも無かったし…）

シンボリック制約からニューラル制約への変換方法

Neuro-symbolic Executionを実行しているとシンボリック制約とニューラル制約の2種類の制約が混合する。混合した制約を解くためにNeuExはシンボリック制約をニューラル制約（正確にはロス関数 $L$ ）に変換する。変換はTable IIに従う。

f:id:katc:20190607003245p:plain — Table II

ロス関数 $L$ は上述の性質を満たすように人為的に定義されている。

Neuro-symbolic Executionにおける制約充足アルゴリズム

f:id:katc:20190609024330p:plain — Algorithm 1

※アルゴリズムの説明は省略。

（友利注：書くの飽きてきた…。方針としては、DAG上で変数の依存関係が独立なコード片を順々にNeural Executionし、最後にそれらの制約をシンボリック実行の結果とマージという感じみたいね。）

評価

NewExの実装は以下の構成。

KLEE v1.4ベース（友利注：KLEEの2019/06/09時点の最新版はv2.0（2019年5月リリース）。1つ前のバージョンが1.4）
libcには KLEE-uClibc を採用（友利注というか疑問：ソースコードが入手可能であることを前提にしてる？）
SMTソルバーはZ3
- （友利注：KLEEはソルバーを選べる https://klee.github.io/docs/solver-chain/ ）

評価は以下の観点で行った。

(a) KLEEに対する効率性
- 素のKLEEと比べてNeuExはより多くの脆弱性を見つけるのか？（友利注：原文よりも目的を明確に意訳した）
(b) Neural Modeの効用
- Neural Modeの呼び出し回数、エクスプロイト生成数、実行時間はどうか？
- 友利注：Neural Modeが一度も呼ばれなかったり、何もエクスプロイトを生成してなかったり、Neural Modeの実行時間が卓越したりするオチもあり得るので大事な観点。
(c) 既存のシンボリック実行テクニックとの比較
- 友利注：素のKLEEを最適化するとKLEEよりも成績が良くなるのは自明なので、同一環境で既存の最適化手法（今回はLESEと、Veritestingを採用したangrの探索モード）と比較するのは必須。

実験条件

機械学習フレームワークはTensorFlowを採用した。
活性化関数 $\mathbf{f}$ は正規化線形関数（ReLU） $f(u) = max(u, 0)$ を採用した。
マシンは40-core 2.6GHz 64GB RAM Intel Xeon machine。

(a) KLEEに対する効率性

KLEEに対してNeuExはCVPに到達できた数とその早さにおいて優位であり、エクスプロイトの生成数（友利注：脆弱性を再現できた数）においても優位。

f:id:katc:20190609031848p:plain — Table III

f:id:katc:20190609033429p:plain — Fig. 7, 8

(b) Neural Modeの効用

Neural Modeは使用されたし、いくつかのCVPに到達できているし、少数のエクスプロイトを生成したことが分かる。

f:id:katc:20190609033115p:plain — Table IV

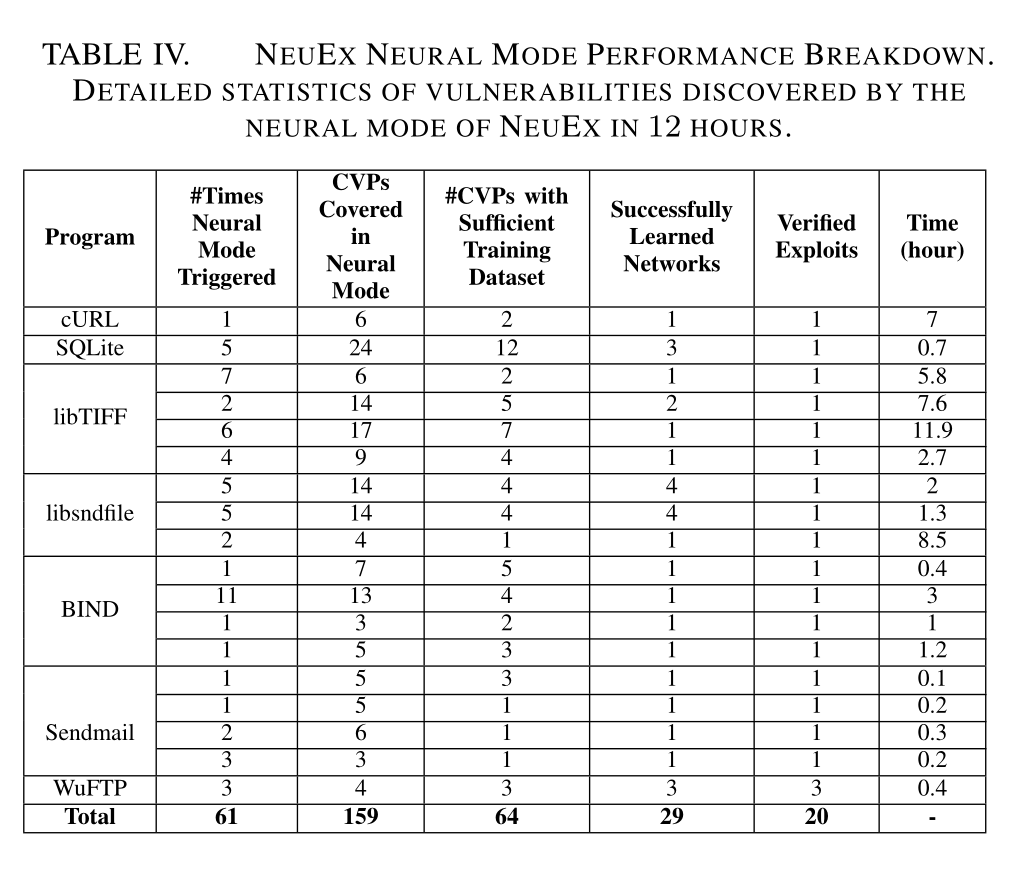
(c) 既存のシンボリック実行テクニックとの比較

LESE (ISSTA 2009)（バイナリのループに関する推論を行うテクニック）
- LESEの実装が公開されていないので、論文に掲載された実験条件と同等環境を用意し、同じベンチマークを実施した。
- NeuExはNeuro Modeのみ使用した。変数の関係性の学習においてニューラル制約のアイデアがLESEに対して優位であることを確認するため。
- 脆弱性検出の早さについては、NeuExはLESEに対して平均2桁倍だった。
Veritesting (ICSE 2014)（友利注：静的シンボリック実行と動的シンボリック実行を複合するなど）
- Veritesting の実装（友利注：MergePoint）が公開されていないので、Veritestingを再実装している angr と比較した。
- Veritestingは脆弱性の箇所を教える必要あり。同じ開始条件で実行するとNewExは34分で脆弱性を検出したが、angrは12時間以内に検出せず。angrでは198の外部関数の呼び出しがあったがいずれも対応せず。

結論

NeuExはニューラルネットワークを用いてプログラムの振る舞いを近似する制約を学習する。
Neuro-symbolic Execition はシンボリック制約とニューラル制約の複合した制約を解くことができる。
素の動的シンボリック実行に対してバグの検出件数が94％増加した。

所感

単純なネットワークでもプログラムの断片における変数間の関係（ $N: \mathbf{x} \mapsto \mathbf{y}$ ）を学習できるんだなぁという知見を得た。ニューラルネットワークの実装に関する以下の記述を読んでも、入出力の次元数、隠れ層の次元数と層数が書かれてなかったのでどの程度のネットワークがあればいいのかがワカラン。 Neural ModeとNeuSolvだけを見ても新規性があるかどうかが気になる。

Training. Next, the neural constraint inference engine takes 80% of all the generated sample sets for training the neural net. We use a standard MLP architecture with Relu activation function implemented in Python and Google TensorFlow [29] with a total of 208 LOC. We use the early-stopping strategy to avoid over-fitting. We test the remaining 20% of the sample set on the learned neural net to measure its accuracy. We continue the training until we achieve at least 80% accuracy. If the loss of the trained neural net does not start decreasing after a threshold of 50 epochs, we discard the search for an exploit for the corresponding CVP.

Neural ModeとNeuSolvはシンボリック実行に依存していないように見える。 $\mathbf{x}, \mathbf{y}, L(\mathbf{y})$ を得られれば適用可能に見える。 $\mathbf{x}, \mathbf{y}$ はランタイムで得られ、 $L(\mathbf{y})$ はCVPを元に機械的に計算可能。ならシンボリック実行だけでなくファジングでも適用できるのでは？

私の理解が正しければ元のプログラム自身も関数 $N$ を持っているとみなせるので、ニューラルネットワークを用いて $\dfrac {\partial N}{\partial \mathbf{x}}$ を計算しなくても、元のプログラムを使ってそれを計算できる気がする（まぁ実装して検証すればいい話）。よく分からなくなってきた…😇

付録：多層パーセプトロンの復習

ニューラルネットワークの構成方法の1つである多層パーセプトロンについて復習しよう。

まず多層パーセプトロンのネットワーク構成について復習する。

多層パーセプトロン

層数 $L$ の多層ネットワークを考える。層 $l+1$ のユニットの出力 $\mathbf{z}^{(l+1)}$ は、1つ下の層 $l$ のユニットの出力 $\mathbf{z}^{(l)}$ から

$\mathbf{u}^{(l+1)} = \mathbf{W}^{(l+1)} \mathbf{z}^{(l)} + \mathbf{b}^{(l+1)}$

$\mathbf{z}^{(l+1)} = \mathbf{f}(\mathbf{u}^{(l+1)})$

のように計算される。ここで、 $\mathbf{W}$ は重み、 $\mathbf{b}$ はバイアスとよばれ、 $\mathbf{w}$ をこれらのパラメータすべてを成分に持つベクトルとする。

ネットワークの最終出力 $\mathbf{y}$ は

$\mathbf{y} \equiv \mathbf{z}^{(L)}$

と得る。

次には学習方法を復習する。

確率的勾配降下法

入力 $\mathbf{x}_n$ を与えたときのネットワークの出力 $\mathbf{y}(\mathbf{x}_n; \mathbf{w})$ がなるべく訓練データ $(\mathbf{x}_n,\mathbf{d}_n)$ の $\mathbf{d}_n$ に近くなるように $\mathbf{w}$ を調整する。これを学習と呼ぶ。

ネットワークのパラメータ $\mathbf{w}$ の調整には

$\mathbf{w} ^ {(t+1)} = \mathbf{w} ^ {(t)} - \varepsilon \frac{\partial}{\partial \mathbf{w}} L(\mathbf{w})$

を用いる。ここで $t$ をエポック、 $L$ を誤差関数とする。